終於來到大家所最害怕的Dynamic Programming也就是中文所說的「動態規劃」，希望各位讀者到這邊能依舊繼續堅持下去啦，我會盡力用最簡單的方式講述給大家聽。

其實DP跟遞迴有蠻緊密的關係，以下我們來用大家最常使用的費波那契數列來探討動態規劃吧！

遞迴中的費波那契數列

費波那契數列就是指說我這一項的值就是前兩項值的和「1、1、2、3、5、8、13···」用公式來表示就是F(i)=F(i-1)+F(i-2)，還記得我們在遞迴的文章中有提到，我們需要先定義好BaseCase才不會讓Call Stack Overflow，這邊我們的Base Case是甚麼呢？答案就是F(0) = 0, F(1) = 1，有了這兩個值，我們就可以用遞迴計算出任意的F(i)啦！
以下就是python的遞迴程式碼。

def fibonacci(n):
    if n < 2: return n
    return fibonacci(n-1) + fibonacci(n-2)

還記得遞迴嗎？當我輸入fibonacci(3)的時後，我們會需要fibonacci(2) + fibonacci(1)的結果，fibonacci(1)已經滿足Base Case會回傳1，fibonacci(2)會去計算fibonacci(1) + fibonacci(0)的結果，1跟0也都是Base Case所以會回傳1+0=1，最後把fibonacci(2)+fibonacci(1)加起來也就是，1+1=2。

遞迴的時間複雜度分析

用遞迴來實作費波納氣數列的時間複雜度是多少呢？我們來舉f(5)為例，我們可以發現要得到f(5)我們要先計算f(4)跟f(3)，計算f(4)要先計算f(3)跟f(2)，以此類推，我們可以把圖畫出來。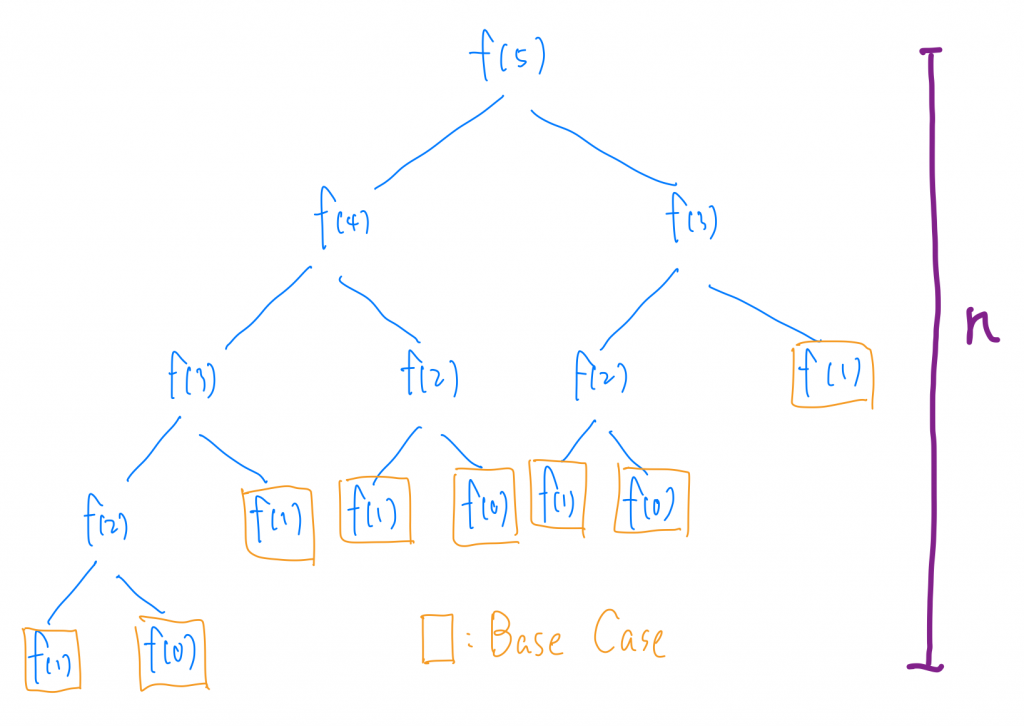

這邊我們可以發現，每一個節點都是一生二的關係，節點數也就是我們需要去計算的次數，我們還可以發現說，樹的高度就是我的n值，用這個為例，就是5。所以高度為5的樹，大約約有2^5個節點，每個節點都代表我計算的次數，所以我們可以知道時間複雜度是2^n。

找出重複計算的節點

難道！我們就不能再更快了嗎？請不用擔心，我們來仔細看一下這張圖我們會發現，其實有很多地方我們都重複計算了，譬如，f(5)我們要計算f(4)跟f(3)，f(4)我們要計算f(3)跟f(2)，所以當我們計算完f(4)，理論上也計算完f(3)，也就不用再多計算一次了。所以下次我遇到f(3)我只需要把計算過的f(3) 回傳這樣就省下很多時間啦！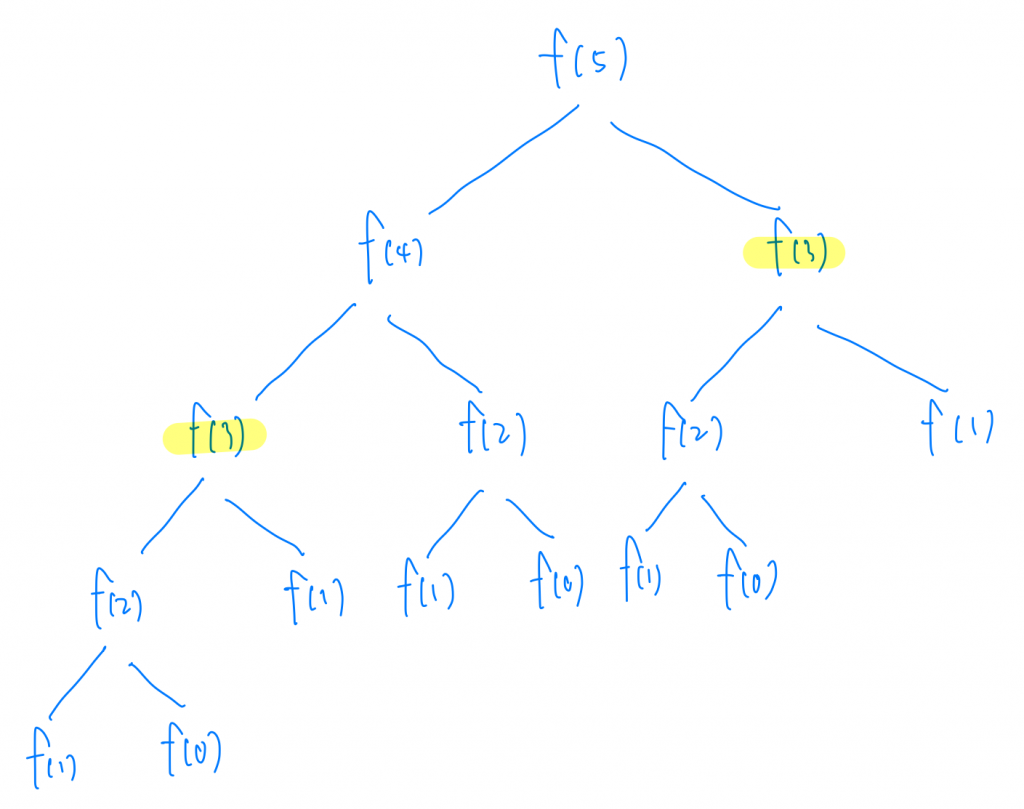

至於要怎麼保存計算過的值，有兩種方法。

Top Down

顧名思義就是從上到下的意思，但每當我計算完一個狀態的值的時候我就存到HashMap中，如果之後有再被重複使用到，我直接從HashMap拿出來就可以啦！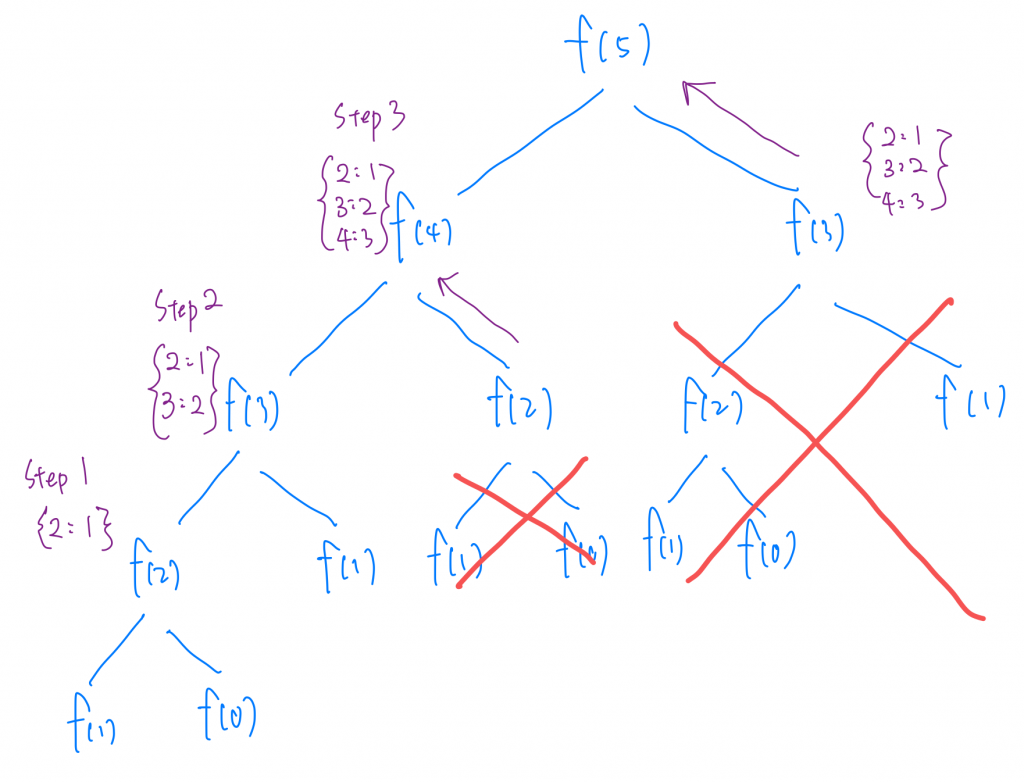

所以當我們計算完f(4)的時候，照理說我們也已經拿到f(3)值了，如果我們在拿到f(3)的值的時候有把他記錄下來，當f(5)要去呼叫f(3)的時候，我不用在重複計算，直接去HashMap裡面拿就可以囉。

Bottom up

Bottom up 就是我們遞迴的想法反過來想，甚麼意思呢？想像一下我們遞迴就是從上往下一直到Base Case在Return回來，那如果我一開始就定義好BaseCase讓他往上到我們要的結果呢？
用圖讓大家理解會簡單很多，我們用一個Array來記錄，Array的index代表f(index)的值，所以我們一開始建立長度是6的array，接著我們將index 0填入0、index 1 填入1，這邊代表f(0) = 0, f(1) = 1，那f(2)也就是說index 2呢？記得我們的定義嗎f(n) = f(n-1)+f(n-2)，所以index 2 的值就是index(1) + index(0)，這樣index 2就算好了，index 3 呢？很簡單了對吧，就是index 2 + index 1，我們最後只需要一直這樣到index 5 答案就出來啦！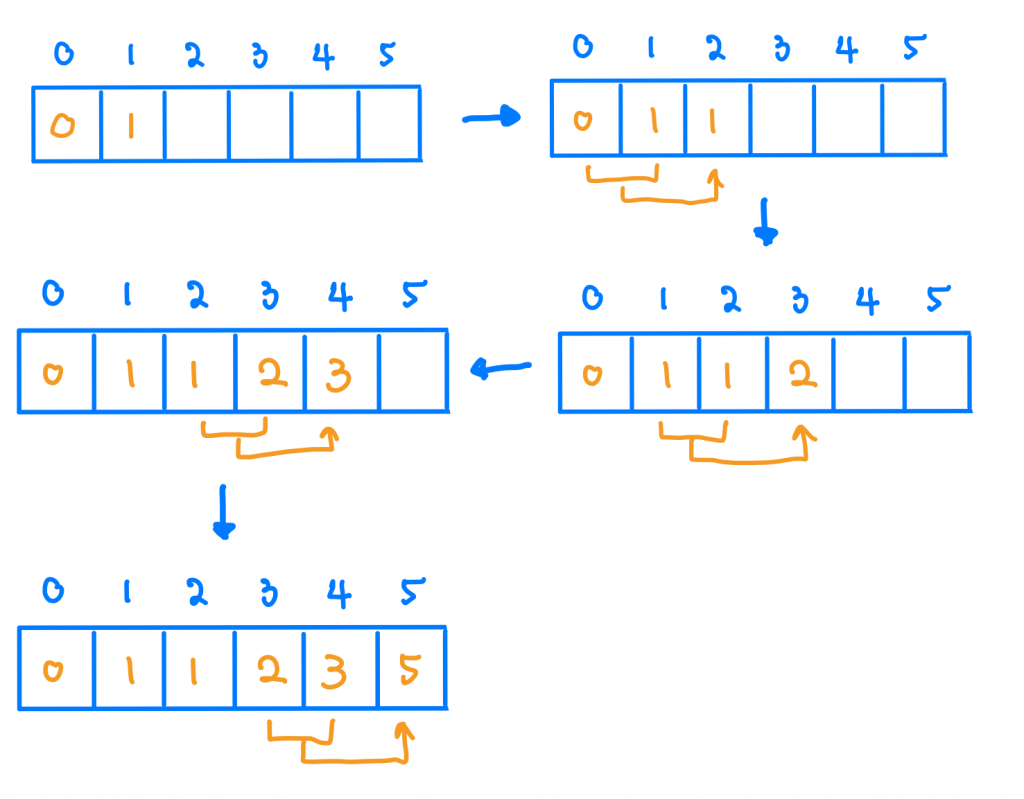

時間複雜度分析

現在我們來看看利用DP後時間複雜度變成多少吧！
我們先從Bottom up的方法開始，其實不難理解Bottom up的方法，我們實際上就是去填滿一個長度為n的Array，然後我的每一次填值的動作都只是把前兩個index的值加起來時間複雜度為O(1)，我要填n次，所以時間複雜度就是O(n)啦！

Top Down的方法呢？我們來思考看看，因為我們在過程中把每次的中間狀態的值都記錄下來，所以原本的樹狀圖就變成高度為n的單邊的樹狀圖，記得前面有說到節點的數量就是我計算的次數，所以時間複雜度也是O(n)囉。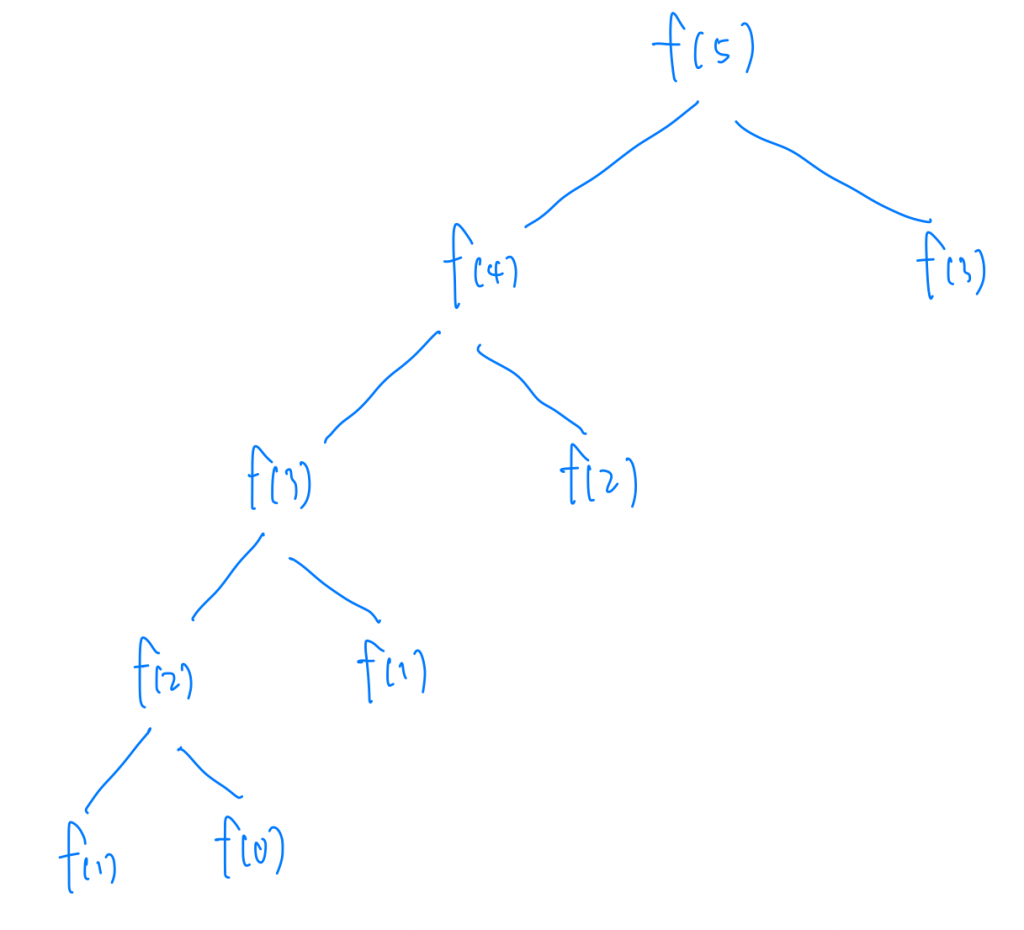

結論

DP的問題其實我認為撇開題目難做的這個想法，他是一個很好去省思問題的一種思想，既可以讓我們訓練抓出重複計算的值把它記起來方便以後使用，也可以用另一個角度反過來去看待這個問題(Bottom up)，雖然說工作上很難會用到這項技巧，但是學起來一定是有益無害的啦！